LLM Quantization? GPTQ vs AWQ

Quantization이란?
Quantization은 연속적인 값을 불연속적인 값으로 변환하는 과정이다. 이 과정은 연산의 복잡도를 줄이고, 메모리의 효율성을 높이고, 전송의 속도를 증가시키는 등의 장점을 가진다. 하지만 Quantization은 원래의 값과 변환된 값 사이에 차이가 발생하므로, 정보의 손실이나 오차가 불가피하게 발생한다. 이러한 오차는 모델의 성능에 영향을 줄 수 있다.
Analogy to Digital Image
Quantization의 개념을 이해하기 위해, 디지털 이미지의 색상 표현과 압축 방식을 예로 들 수 있다. 32비트 풀 컬러 이미지는 매우 높은 색상 해상도를 가지고 있어 수백만 가지 색상을 표현할 수 있지만, 이는 각 픽셀마다 많은 데이터가 필요하며, 결과적으로 이미지 파일의 크기가 커지고 처리 속도가 느려진다. 반면에, 256 컬러 이미지는 색상을 훨씬 적은 범위로 제한하여, 각 픽셀당 필요한 데이터 양을 줄이고, 파일 크기를 줄이며 처리 속도를 빠르게 만든다. 하지만, 이 과정에서 색상의 세밀함과 이미지 품질이 손실될 수 있다.
이러한 색상의 압축에서는 사람의 체감 품질 열화를 최소화하는 기술이 중요하다. 예를 들어, JPEG 압축 방식은 인간의 시각적 민감도를 고려하여 덜 중요한 색상 정보를 감소시키고, 중요한 정보를 보존한다. 이 방식은 데이터 양을 줄이면서도 시각적 품질을 유지하는 데 중요하다.
DNN에서의 Quantization도 유사한 방식으로 작동한다. DNN의 파라미터들은 고정밀도로 표현되지만, 이를 낮은 비트로 줄여 연산을 단순화하고 메모리 사용량을 줄인다. 이 과정에서 모델의 크기가 줄어들고 추론 속도가 증가하지만, 정확도에는 약간의 손실이 발생할 수 있다. 이와 같이 DNN에서의 Quantization은 중요한 파라미터를 보다 높은 정밀도로 유지하고, 덜 중요한 파라미터는 더 낮은 정밀도로 줄여나가는 방식으로 진행된다.
PTQ (Post-Training Quantization)
DNN에서는 Quantization을 통해 모델의 크기를 줄이고, 연산 속도를 높일 수 있다. 하지만 DNN의 파라미터는 학습 과정에서 결정되며 Training에 앞서 이들 파라미터가 어떠한 범위를 가질 지 알 수 없다. 또한 낮은 정밀도로 학습하는 것은 아직 잘 연구되지 않은 분야이다. 따라서 현재는 이미 학습된 모델에 Quantization을 적용하는 후처리 방식(Post-training Quantization)이 많이 사용된다.
LLM.int8()
TL;DR
- MatMul을 독립적 Vector Inner Product로 분해하여 각각을 Normalize하여 full scale int8으로 sampling
- 하지만 이 방법을 적용하는 과정에서 6B Parameters 이상의 규모에서 parameter에 outlier의 분포가 증가함 (6.7B에는 거의 모든 Transformer Layer와 전체 중 75%의 layer에 이러한 것들이 생김)
- 그런데 이러한 outlier는 전체 Parameter의 약 0.1%이지만 성능에 매우 큰 영향을 줌
- 따라서 이러한 outlier는 그대로 남겨두고 (fp16) 나머지만 vector-wise quantization을 적용하니 성능에 별차이 없이 모델의 크기를 크게 줄일 수 있었음
Vector-wise Quantization
- Matrix Multiplication은 서로 독립적인 Column과 Row의 Inner Product (dot product)로 볼 수 있음.
- 각각의 inner product쌍에 독립적인 normalization constant를 적용 전체 Matrix에 대한 각 행과 열의 normalization constant vector를 얻을 수 있음
- 이러한 방법으로 int8 MatMul과 normalization constant vector의 outer product를 이용 원래의 output을 구할 수 있음
- 이러한 방법으로 2.7B의 Scale까지 심각한 성능 열화 없이 모델의 사이즈를 줄일 수 있음
- 단, Scale이 커지게 되면서 Outlier가 증가하며 이때문에 Quantization error가 커지게 됨
Beyond 6.7B parameters
- 6.7B Parameter 이상의 규모에 대해서 품질의 열화 없이 이러한 Quantization을 적용하려면 Inference 시의 hidden state에 존재하는 extreme outlier의 emergence를 이해하는 것이 매우 중요
- 예컨데 실험에서는 다른 feature vector 대비 20배 이상이 outlier가 전체 transformer layer의 약 25% 정도에만 나타나다가
- 6.7B에 이르러서는 모든 transformer layer에 나타나고 이외 모든 sequence dimenssion 중 75%에 나타나게됨
- 하지만 이러한 outlier는 높은 규칙성을 보였음.
- 예를 들어 6.7B의 규모에서 약 150,000개의 outliers가 나타났으나 이들 모두 6개의 feature dimension에 집중
- 이들 outlier는 전체 입력 Feature의 약 0.1%를 차지하지만 이들 Outlier를 제거할 경우 심각한 성능 열화가 발생함을 확인 (600 ~ 1000% Perplexity degradation)
- 이는 2.7B에서 보았던 0.1%의 perplexity degradation과 너무나 큰 차이임
Mixed-precision decomposition (Solution for Outlier)
- 0.1%의 outlier에 대해서 FP16으로 처리하고 99.9%에 대해 8-bit matmul로 처리
- 이렇게 Mixed Precision Decomposition과 Vector wise quantization의 2가지 요소를 결합한 것을 LLM.int8()이라 함
LLM.int8() Key Concept
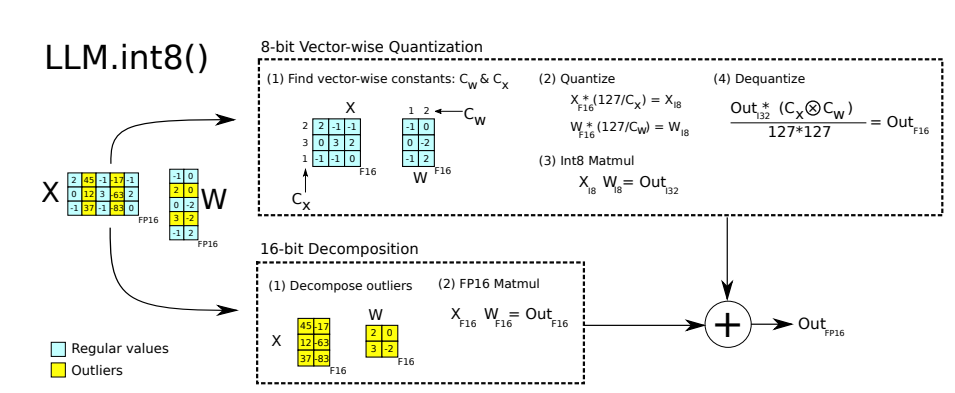
- FP16의 X와 W가 주어졌을 때 feature와 weight은 outlier와 regular values로 나뉘어진다.
- outlier의 sub-matrices는 fp16 그대로 두고 처리
- regular values의 sub-matrices는 vector-wise normalization constant를 구하여 이를 통해 full-scale int8으로 sampling함
limitation
1. Int8 데이터 형식만을 대상으로 연구하였다는 점, 이는 현재 GPU에서 지원되는 유일한 8bit 형식이기 때문임
2. 175B 규모의 모델까지만 테스트 되었다는 점, 이러한 방법이 더 큰 규모의 모델에서 어떠한 영향이 있을지 알 수 없음
3. Attention의 경우 8bit matmul을 적용하지 않았으며 이는
- Attention function 자체는 parameter가 개입되지 않는다.
Softmax(Q@K.T/sqrt(d))@V - Memory footprint를 줄이는 것에 주력
4. Inference에만 초점을 맞춘 연구임. Int8 training에 대한 초기 분석을 별첨에 제공하나 int8 training을 대규모로 진행하는 것은 아직은 매우 어려운 문제임
GPTQ
TL;DR
- layer 단위로 quantization을 수행, 이론적 기반으로 기존의 LeCun 등이 연구한 OBS(1990)방식을 계승,
Layer-wise Quantization and OBC(Optimal Brain Compression)
- 저자들은 과거 Yann Lecun 등이 제안하여 다양한 xNN에 널리 사용된 OBD(Optimal Brain Damage)를 개선한 OBC라는 자신들이 고안한 방식을 활용
- Layer 단위로 최적화를 적용, loss에 대한 2차 편미분인 Hessian matrix를 구하고이 값을 기준으로 weight의 Quantization을 우선순위화
- 각 weight을 위 우선순위에 따라 quantization하고 이에 따라 나머지 Quantize 되지 않은 weight를 update하여 quantization을 보상
Additional Insights
- 위 OBC 기반의 방식은 Hessian에 따라 순서대로 Weight를 Update하였지만 LLM에서 이러한 순서의 영향이 크지 않음을 발견
- 아울러 이와 같이 Weight를 개별적으로 Iteration하면서 Quantizatino하고 이를 보상하기 위해 다른 모든 Weight를 업데이트 하는 방식이 비효율적이며 다행히 이를 보다 효율적으로 처리할 수 있는 Patch로 나누고 이 Patch에 대한 처리 결과를 전체 Matrix에 한번에 반영하는 형태로 효율화 할 수 있음
- Hessian 값은 매우 작은 값을 갖기도 하기 때문에 수치 연산의 안정성을 크게 떨어뜨리고 오차가 커지게됨. 이를 Cholesky Reformulation을 통해 방지함
Result
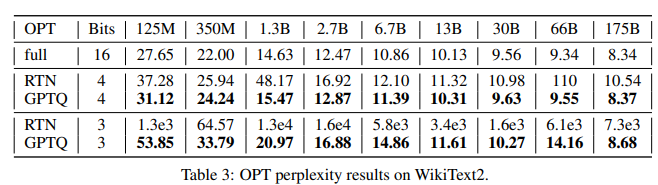
- RTN(Round To Nearest) 방식 대비 우수한 성능을 보임
- Parameter 규모가 클 수록 full precision 성능과 Gap이 크지 않음 (Large 모델일 수록 유리)
Limitation
1. Activation Quantization은 고려되지 않음
2. 연구의 성능 및 효과는 Generative Tasks에 한정 (Classification, NER 등 기타 NLP의 검증 필요)
3. Memory Bottleneck을 해소하여 속도를 개선하긴 하였으나 연산 복잡도를 줄인 것은 아님
Wrap-up
- 앞서 소개한 LLM.int8() 대비 높은 압축률의 sub 8bit quantization 이지만
- Calibration을 위한 Input data가 필요하고 더 복잡함
- 그리고 Larger Scale로 갈수록 생각보다 RTN랑 별차이가 나지 않음
AWQ [slide]
- 기본적으로 LLM.int8()과 유사한 관찰에서 접근
- 전체 weight 중 0.1 ~ 1%의 salient weight가 존재하며 이들의 값의 error 혹은 정밀도 손실은 다른 weight보다 더 큰 영향을 줌
- 단, LLM.int8()는
weight의 magnitude를 기준으로 outlier를 선정하였다면AWQ에서는 weight에 대응한 Activation output의 magnitude를 기준으로 사용 - Quantization function을 Q(w)로 아래와 같이 정의

- 위 Qauntization에서 임의 scale factor s를 추가하여 weight과 입력 x에 적용할 경우 Quantization Error는 s term에 반비례함을 보임 (위 이미지의 Err’ = A’ * RoundErr * 1 / s)에 의해..
- RoundErr가 크게 변하지 않는 선에서 s를 1보다 큰 값 범위에서 증가 시킬 경우 전체 Quantiztaion Error가 감소해야 함
- optimal scale factor를 얻기 위한 loss 함수는 아래와 같이 나타낼 수 있는데,
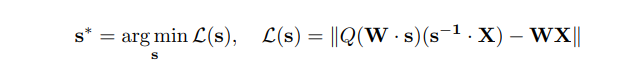
- 여기서 quantization함수는 미분가능하지 않다. 따라서 Gradient Descent에 의한 방법은 적용이 불가하며
- scale을 1부터 activation의 크기 값까지 fast grid search를 수행하여 최적의 값을 찾음
Result
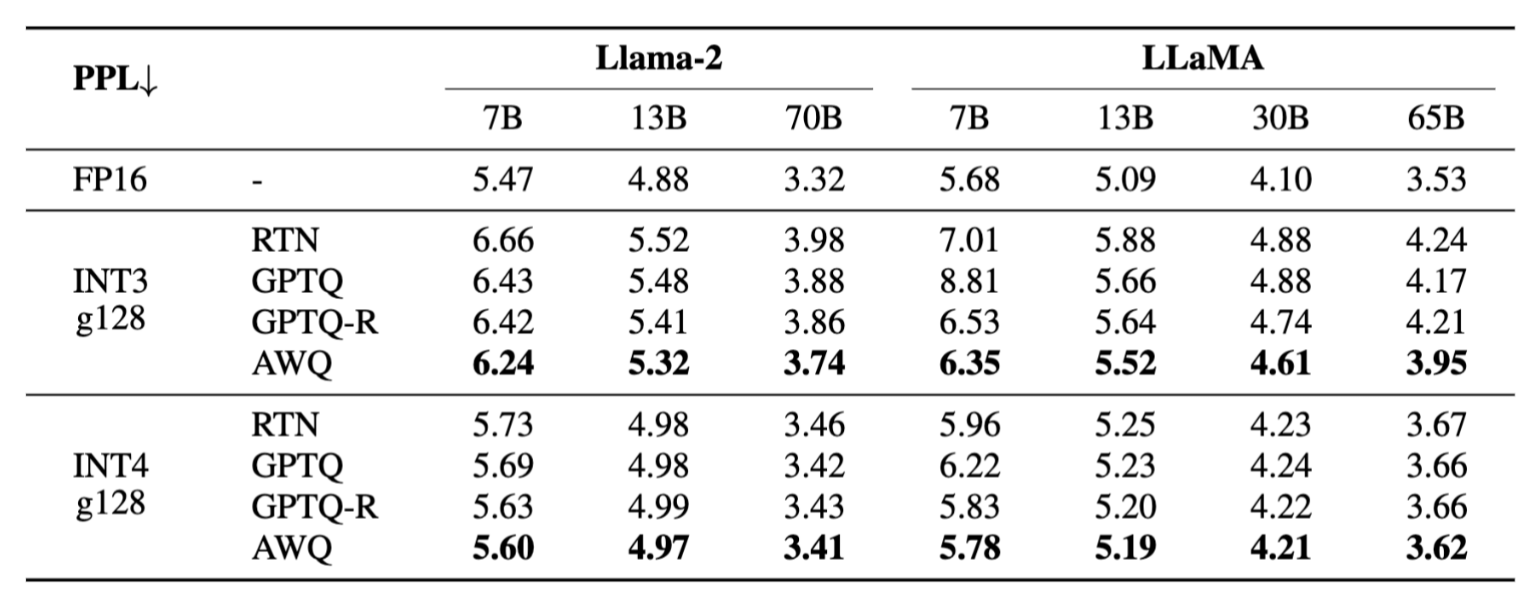
- RTN, GPTQ, GPTQ-R (앞의 설명에서 GPTQ의 weight 최적화 ordering을 적용한 것) 대비 전체 모델 사이즈에서 우수한 성능을 보임
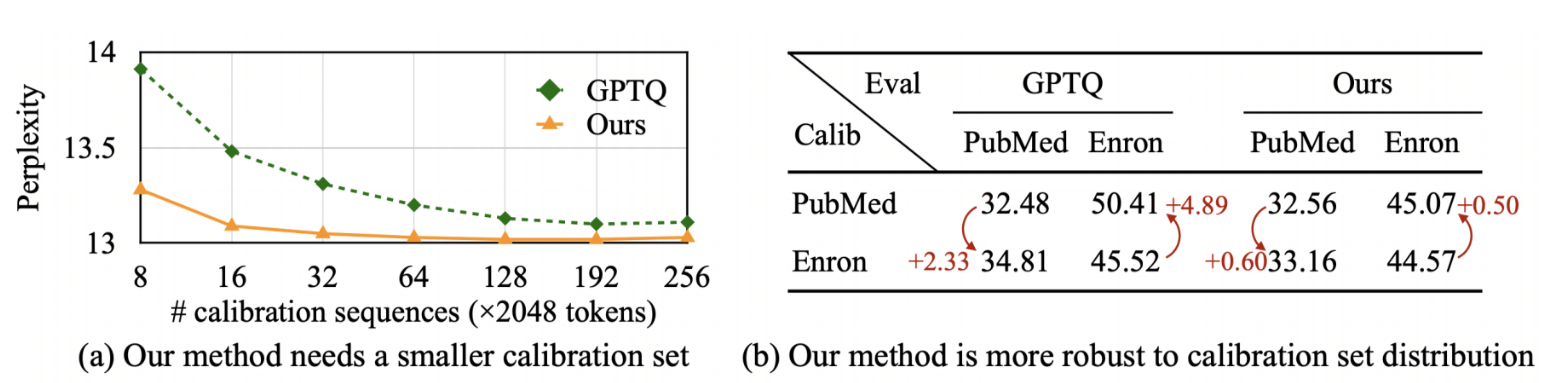
- Calibration 데이터 의존도가 낮음 (적은 데이터만으로도 적용가능)
- Calibration 데이터 차이에 따른 (PubMed vs Enron) 성능 편차가 적음 (예 Wikitext로 Cal하면 Wikitext에는 성능이 유지되나 다른 데이터에 대한 성능은 열화되는…)
- 일반 GPU (4090)에서도 x3.3배의 성능 향상을 보임
Wrap-up
- 7B ~ 13B 모델에서 Original과 다소 차이를 보였던 RTN이나 GPTQ 대비 전반적인 성능 개선 기대
- Single Precision으로 CPU에서 제공되는 AVX나 SIMD 등을 통한 가속에 있어서 유리할 것으로 보임
- 아직 GGML에서 지원되지 않고 있음.
Comparison (LLM.int8() vs GPTQ vs AWQ)
| LLM.int8() | GPTQ | AWQ | |
|---|---|---|---|
| precision | Mixed-Precision (int8 + fp16) | Mixed-Precision (int4,int3 + fp16) | Single Precision (int4, int3) |
| calibration data | No | Yes | Yes |
| implementation | bitsandbytes | AutoGPTQ | FasterTransformer, HuggingFaceTGI,vLLM, Neural Compressor |